TRILATERATION

Sometimes referred to as triangulation, trilateration is a more accurate description of the process by which GPS map co-ordinates are established.

Think back to physics lessons in your school days. (I can just about remember mine). Is the formula below familiar?

Distance = Speed x Time

That is essentially how the system manages to work out the GPS map co-ordinates. The GPS signal travels at the speed of light (299,792,458 m/s). The speed can vary slightly for reasons I will not go into here, but essentially, for our purposes, it can be regarded as a constant figure. Every GPS satellite is equipped with an extremely accurate atomic clock, so the system knows at which time the signal is sent from each satellite. The GPS receiver also keeps track of the time, albeit not as accurately as the atomic clocks on the satellites, so we know the times at which the signals reach the receiver. The distance is therefore the product of c (the speed of light - which can be regarded as a constant) and the time difference between:-

When the satellite sent the signal, and
When it reached the receiver.

Each satellite transmits its identity, its position, and the time of transmission. Additionally, it transmits information on the position of other satellites. Using the calculation shown above, GPS comparisons are made between the satellite signals. The distance from each satellite to the receiver can be calculated using the principle of trilateration (the determination of a distance from three points). With information from 3 satellites, a 2D position fix is possible. The assumption is that the receiver is on the Earth Geoid (effectively sea level). When you add a fourth satellite signal, it becomes possible to also calculate the height above sea level, or for aviation applications, the altitude of the receiver, and you get a 3D position fix. By continually monitoring the position and the way it changes over a measured period of time, it is therefore also possible to determine speed and direction of travel.

Sometimes referred to as triangulation, trilateration is a more accurate description of the process by which GPS map co-ordinates are established.

How does Trilateration actually work?

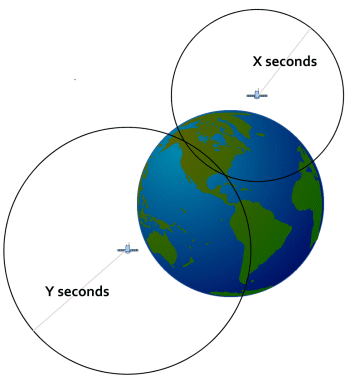
Forget for the moment that the earth is a sphere and consider it as a flat disc. In the illustration to the right, the receiver has acquired signals from two satellites. The first one has taken X seconds to travel from the satellite, and the second one has taken Y seconds. We know from the formula above how far each satellite is from the receiver, and if we draw two circles with radii X and Y respectively, we see the possible positions of the receiver traced out by the two circles. The circles intersect in two places, so there are 2 possible positions where the receiver could be. That is why it is not possible to determine a position with only 2 satellite fixes.

If you click on the "3D Position Fix" box, you can see that when a signal from a third satellite is also received, there is no longer any doubt about which position is the correct one.

Trilateration! It's that simple.

Of course, the earth is a sphere and not a flat disc, so it is a little more complicated than I have described, but the same principle applies.

Accuracy of position

I mentioned earlier that the receiver was not as accurate as the atomic clocks on the satellites. When you consider that the average time taken for a satellite signal to reach the earth is only about seven hundredths of a second, it would need a time error at the receiver of only one hundredth of a second to give a position potentially out by almost 2,000 miles. Just think, that is the smallest increment used in measuring times taken in competitive sports. The time must be accurate to within 0.00000003 seconds to achieve a positional accuracy within 10m. Fortunately, the system is able to correct for time inaccuracies at the receiver.

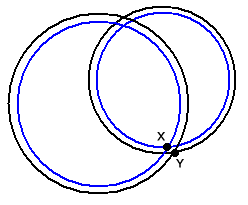
Signal time inaccuracy with 2 satellites

Supposing the receiver time is slightly fast with respect to the accurate satellite times. That means that the system calculates the time taken to travel from satellites to receiver is longer than it actually is.

If you look at the diagram, the inner blue circles represent the actual times. The outer black circles represent the inaccurate times. This gives a position of Y when it should be X. With two satellite signals, there is no way of telling that there is a time error.

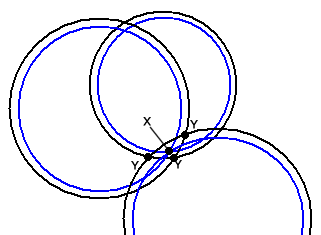
Signal time inaccuracy with 3 satellites

However, when you add the signal from the third satellite, it becomes apparent that you have 3 points of intersection of the black outside trilateration circles with the time error giving 3 position Y's.

The system can then correct for the time error (which is constant for each satellite since all the satellites use very accurate atomic clocks) until the circles converge on a single point (point x), the correct position.

With the 2D position accurately established, the height or altitude can then be calculated using the signal from a fourth satellite. GPS receivers routinely track many more than 4 satellites.